|
Booleaanse logica ligt aan de basis van de digitale elektronica. Zoals het woord zelf al aangeeft gaat het hier om een logisch denkproces. Dit denken krijgt steeds meer plaats in de elektronica en door de stijgende informatisering zal deze trend in de toekomst nog meer toenemen. Daarom ook hier aandacht voor dit het onderwerp. |
||||||||||||||||||||||||||||||||||
|
Wat we tot nu toe gezien hebben is “gewone” analoge elektronica. We stappen in dit hoofdstuk over naar digitale technieken. Wat is het verschil ? |
||||||||||||||||||||||||||||||||||
|
Voor de gewone man valt dit niet op, want het digitale is in de natuur niet direct zichtbaar. Alle fysische grootheden lijken ons analoog van aard. Analoge grootheden kunnen op een gelijkmatige en continue wijze uitgedrukt worden, bijvoorbeeld de temperatuur gedurende de dag. Deze verandert in functie van de opwarming door de zon en zal bijv. in een paar uur van 12 ° naar 25° kunnen stijgen, maar nooit in een tijdspanne van µs. |
In de numerieke of digitale elektronica bestaat zo een geleidelijke evolutie niet. We werken met grootheden die maar twee toestanden kunnen aannemen. Het kan warm of koud zijn, wit of zwart, spanning voeren of niet, met andere woorden JA of NEEN. De waarden vertegenwoordigen een staat of toestand, en we stellen deze toestand voor met het cijfer “0” of “1”. In de elektronica vertalen we dit naar een aanwezigheid van spanning “1” of niet, “0”. Er is dus geen continue evolutie mogelijk, er bestaat enkel discontinuïteit in de toestand. |
|||||||||||||||||||||||||||||||||
|
Even over het tellen : |
||||||||||||||||||||||||||||||||||
|
Dat de mens tien vingers of tenen heeft kan toeval zijn, maar het heeft de mens aangezet om het tellen daarop te steunen. Dit is voor ons evident maar in de natuur is er geen enkel verder verband. We zijn gewoon om het cijfer 10 als grondtal te gebruiken. |
Het principe is eenvoudig. We beschikken over tien symbolen: (0,1,2,3,4,5,6,7,8,9); gaan we verder dan 9 dan beginnen we opnieuw maar plaatsen het cijfer 1 vooraan (10). Dit worden dan de tientallen. Wees gerust: dit zal wel geen vraag voor het examen zijn ! |
|||||||||||||||||||||||||||||||||
|
Nu hebben we wel een probleem, want bij ons logisch systeem gebaseerd op de elektriciteit hebben we geen tien symbolen maar slechts twee. De aanwezigheid of afwezigheid van spanning wordt onder de vorm “1” of “0” genoteerd. |
Hier moet iets op gevonden worden. We passen onze nummering aan op die twee mogelijke toestanden en gebruiken daarvoor de cijfers “0” en “1” of basis 2. |
|||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||
|
(NB Om deze tabel duidelijk zichtbaar te maken is het misschien nodig om in je browser een groter lettertype te nemen.) |
||||||||||||||||||||||||||||||||||
|
In de tabel hierboven werden de machten van twee en de overeenstemmende decimale waarden overgebracht. De tabel stopt bij 25, maar er is natuurlijk geen beperking. |
||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
Omgekeerd, de omzetting decimaal naar binair : |
||||||||||||||||||||||||||||||||||
|
Hiervoor gebruiken we de methode van opeenvolgende delingen.
|
||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||
|
Voorbeeld : |
||||||||||||||||||||||||||||||||||
|
Het getal 78 in basis 10 omzetten naar basis 2 : |
||||||||||||||||||||||||||||||||||
|
Het resultaat is 1001110. (De rest van deling 78 is het minst beduidend van het binair getal). Merk verder de volgorde van de rode cijfers op. |
|
|||||||||||||||||||||||||||||||||
|
Hexadecimale aanduiding : |
||||||||||||||||||||||||||||||||||
|
De hex code bevat 16 tekens, dan zijn de getallen dus in basis 16. De overeenstemmende tabel staat hieronder.
Hernemen we het zelfde voorbeeld en zetten dit om naar hex code: vb. 78 om te zetten naar basis 16: |
||||||||||||||||||||||||||||||||||
|
Het resultaat is 4E |
|
|||||||||||||||||||||||||||||||||
|
Er zijn ook nog andere basisgetallen mogelijk vb: octaal |
||||||||||||||||||||||||||||||||||
|
Boleaanse logica : |
||||||||||||||||||||||||||||||||||
|
Beter dan een lange uitleg, een voorbeeld. |
||||||||||||||||||||||||||||||||||
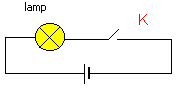 |
Links staat een eenvoudig schema. Een lamp staat in serie met een bron en een schakelaar “K“. |
|||||||||||||||||||||||||||||||||
|
Het is evident dat als k=1 is, het lampje brandt en als k = 0, het lampje niet brandt. Men kan een tabel opstellen die een samenvatting geeft van de verschillende mogelijke toestanden. Zo een tabel wordt de WAARHEIDStabel genoemd. |
||||||||||||||||||||||||||||||||||
|
k is de variabele, 0 is open en 1 is gesloten. |
|
|||||||||||||||||||||||||||||||||
|
De bewerkingen en logische operatoren : |
||||||||||||||||||||||||||||||||||
|
De moderne elektronica laat ons toe met bestaande componenten, complexe logische kringen op te bouwen die uiterst snel logische bewerkingen kunnen uitvoeren. Deze componenten zijn als geïntegreerde schakelingen beschikbaar in alle mogelijke basisvarianten. Steeds complexere kringen worden als één basiscomponent op de markt gebracht. Men gebruikt verschillende technologieën, maar hier beperken we ons nu voor de eenvoud tot het klassieke “TTL” systeem dat werkt op 5V gelijkspanning. Met spanningen van 5 of 0 volt aan de ingangen geven we de door de kring te verwerken logische toestanden. Meestal gebeurt dit via een weerstand maar voor ons gemak tekenen we deze weerstanden niet als dat niet strikt nodig is. We gaan nu over naar de basiselementen . |
||||||||||||||||||||||||||||||||||
| Invertor poort | ||||||||||||||||||||||||||||||||||
|
Als we een spanning van +5 volt aan de ingang leggen, verschijnt 0 volt op de uitgang. Omgekeerd, 0 volt op IN geeft +5 volt op OUT. |
|
|||||||||||||||||||||||||||||||||
| EN poort of AND | ||||||||||||||||||||||||||||||||||
|
In dit voorbeeld zien we twee ingangen (of meer) en één uitgang. Weze ingang e1 en e2 en één enkele uitgang “Out”. Meer concreet, herinner je het schema met het lampje, maar nu met twee schakelaars in serie. Het is duidelijk dat BEIDE schakelaars MOETEN gesloten moeten zijn opdat het lampje zou branden. Dit is in de laatste lijn van de tabel te zien. Voor ALLE andere mogelijke toestanden is de uitgang 0 “nul”. |
|
|||||||||||||||||||||||||||||||||
| OFF poort of OR | ||||||||||||||||||||||||||||||||||
|
Terug twee in (of meer) en één uitgang. Wat concreter: hernemen we het eerste schema maar nu met twee in parallel geschakelde schakelaars e1 en e2. Het lampje zal slechts dan doven als BEIDE schakelaars OPEN zijn. In ALLE ander gevallen brandt het lampje. |
|
|||||||||||||||||||||||||||||||||
|
De NAND poort (zeer veel gebruikt)
of EN/ NIET poort |
||||||||||||||||||||||||||||||||||
|
Opmerkzaam als we zijn, herkennen we meteen het schema van de AND-poort, gevolgd door een omkeerschakeling. Deze combinatie geeft de NAND. Dit is een nieuw symbool waarbij we goed moeten letten op het onderscheid. Het bolletje stelt de invertor voor. |
|
|||||||||||||||||||||||||||||||||
|
De NOR poort
of OFF / NIET poort |
||||||||||||||||||||||||||||||||||
|
Gelijkaardige redenering als bij de NAND poort. |
|
|||||||||||||||||||||||||||||||||
| Poort OFF EXCLUSIEF of XOR | ||||||||||||||||||||||||||||||||||
|
Een wat moeilijker circuit. Voor de ingangssignalen op de klemmen komen worden ze omgekeerd (nul wordt één…). Het resultaat is dat de uitgang slechts dan één wordt wanneer de niveaus op de ingangen VERSCHILLEND zijn. |
|
|||||||||||||||||||||||||||||||||
| XNOR | ||||||||||||||||||||||||||||||||||
|
Het omgekeerde van de XOR. Ook wel complement genoemd van de XOR. Het resultaat is dat op de uitgang slechts dan één wordt wanneer de niveaus op de ingangen gelijk zijn. |
|
|||||||||||||||||||||||||||||||||
|
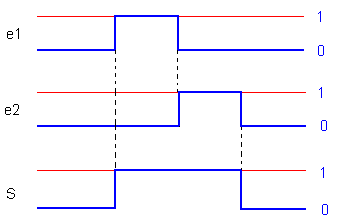
Indien we één en ander met een oscilloscoop zouden gaan bekijken dan zien we spanningsvormen als hieronder aangegeven ( vereist minstens een drie-kanaalsscoop). Bepaal eens welk van de hierboven beschreven digitale schakelingen uit deze signalen terug te vinden is. |
||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||
|
Het antwoord: de uitgang “s” is slechts dan “hoog” als BEIDE ingangen “hoog” zijn. Het gaat hier dus om een exclusief-OR-poort. |
||||||||||||||||||||||||||||||||||
|
Nog wat meer informatie : |
||||||||||||||||||||||||||||||||||
|
Nu gaan we eigenschappen van de logische operatoren zien, of de fundamenten van de Boleaanse logica (een mond vol). Of je voor het examen zover moet gaan laten we in het midden. |
||||||||||||||||||||||||||||||||||
|
Eigenschap van de EN (AND) functie, ook wel als het logisch product met een punt aangeduid “.” |
||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||
|
Eigenschap van de OF (off) functie , ook wel als de logische som met de “+” aangegeven |
||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||
|
Theorema’s van de Boleaanse algebra : |
||||||||||||||||||||||||||||||||||
|
Notaties : |
||||||||||||||||||||||||||||||||||
|
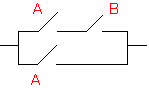
A + AB = A |
 |
|||||||||||||||||||||||||||||||||
|
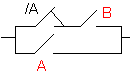
A + |
 |
|||||||||||||||||||||||||||||||||
|
A (B + C) = AB + AC |
 |
|||||||||||||||||||||||||||||||||
|
A (A + B) = A +AB = A |
 |
|||||||||||||||||||||||||||||||||
|
A + BC = (A + B) (A + C) |
||||||||||||||||||||||||||||||||||
|
Universeel gebruik van de NAND : |
||||||||||||||||||||||||||||||||||
|
NAND is zowat de sleutel om allerhande operatoren samen te stellen. Hieronder zie je hoe een en ander in zijn werk gaat. |
||||||||||||||||||||||||||||||||||
| INVERTOR |
Het volstaat om beide (alle) ingangen met elkaar te verbinden. |
|||||||||||||||||||||||||||||||||
| EN (NAND) |
Een invertor na de AND doet de zaak. Dus het schema hiervoor toevoegen NA de AND. |
|||||||||||||||||||||||||||||||||
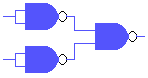
| OFF (OR) |
Gebruik twee invertors voor de ingang van een NAND. |
 |
||||||||||||||||||||||||||||||||
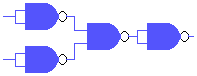
| NOR |
We bouwen verder door nog een invertor achteraan bij te schakelen. |
 |
||||||||||||||||||||||||||||||||
|
Ga dit alles na door op de ingangen alle combinaties van 1 en 0 te plaatsen en kijk dan wat de uitgang wordt. |
||||||||||||||||||||||||||||||||||
|
Dit is (maar) een inleiding tot de digitale wereld. Verder uitbreidingen van wat we tot nu zagen maken het mogelijk complexe kringen als oscillatoren, tellers, comparatoren enz… samen te stellen. Gezien de huidige evolutie – ook in consumententoepassingen – zullen deze digitale technieken steeds meer aan bod komen, vandaar deze toch wat grotere aandacht dan strikt nodig voor het examen. Einde van dit hoofdstuk. Het wordt tijd om de technologische families onder de loupe te nemen. |
||||||||||||||||||||||||||||||||||

