Elektrisch Vermogen

Belangrijk, want het gaat hier over een aspect met weerslag op onze elektriciteitsrekening !

Energie

Zoals de titel laat vermoeden is elektrisch vermogen, een mogelijkheid om energie te leveren.

Je kan best in staat zijn om 100 kg op te tillen. Als je dat in werkelijkheid nooit doet heeft het weinig te betekenen, je beschikt dan wel over het vermogen, maar verder niets. Voer je deze opdracht werkelijk uit, dan heb je energie geleverd.

Hetzelfde gebeurt bij elektriciteit. Als je een elektrische verbruiker niet aan een voedingsbron schakelt, kan je wel zeggen dat de bron in deze belasting de mogelijkheid heeft om energie te leveren. Het is pas bij het werkelijk aansluiten dat er stroom vloeit met als gevolg verwarming of ander energieverbruik gedurende de tijd van de aansluiting.

Het is eenvoudig te begrijpen dat, hoe meer stroom je uit de bron betrekt hoe groter het vermogen wordt, en analoog, hoe meer spanning de bron kan leveren, hoe groter ook het vermogen.

De formule :

Met :
P in Watt
U in Volt
I in Ampere

De energie

De gebruikte energie die je via de elektriciteitsteller zal betalen is evenredig met het vermogen, maar duidelijk ook met de tijd dat je dit vermogen gebruikt: E = W x t

Daar W = U x I wordt de formule   :

      E =   U x I x t

met :
E in Watt sec of JOULE
U in V
I in A

Een voorbeeld van berekening van vermogen

Keren we terug naar het schema zoals bij de studie van de bron gebruikt.

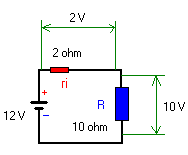We wensen te weten hoe groot het vermogen zal zijn in de weerstand (belasting) in schema links. De belasting bedraagt 10 Ω . De generator zelf heeft een inwendige weerstand van 2 Ω.

1 – We moeten de werkelijke spanning over de belasting kennen (R) en hiervoor rekening houden met de ri van de bron. Dus is kennis van de stroom die door beide weerstanden loopt, onontbeerlijk.

2 – berekenen we eerst de stroom in deze kring

3 – De spanning over R wordt dan:

U = R x I      U= 10 x 1 = 10 V

4 – Het vermogen dat de belasting (R) zal verbruiken wordt dan:

P = U x I     P= 10 x 1  = 10 W

PM: de energie (te betalen) per uur is 10 W uur.

Wat is nu het vermogen dat de bron zelf levert?

Dit is eenvoudig te berekenen.
We weten dat I = 1 A, dat U = 12V, volgt hieruit:

P = U x I    P= 12×1 = 12 W

12 W geleverd door de generator of bron, 10 W wordt door de belasting (R) verbruikt. Wat nu met het verschil? De Ri veroorzaakt een verlies van 2W.
Dit is zuiver verlies onder de vorm van warmte in de inwendige weerstand Ri.

Het verlies ( of moet je zeggen de verspilling ), in de inwendige weerstand is nooit gewenst. Je kan een controle doen door (als je met voldoende grote vermogens werkt) door met de hand te voelen aan de batterij.

Verlies in de bron moet gezien worden als een rendementsverlies. Dit rendement bepalen we zo:

Op 12 W wordt 10 W effectief verbruikt, op 100 W (100%) wordt dat :

Andere formules voor het berekenen van het vermogen :

P= U x I is niet de enige formule. Door gebruik te maken van de Wet van Ohm kunnen we volgende formules afleiden:

Probeer dit even uit.

           U²
P =    ——
           R

Met :

P in W
I in A
R in ohm

P =   R x I²  
 

Nemen we opnieuw het voorbeeld hierboven.

Bereken het vermogen dat door R wordt opgeslorpt :

1st geval

2 de geval

Tot zover de studie van het vermogen. Dit zijn belangrijke formules die je goed moet begrijpen en onthouden. Uit het hoofd leren is niet aangewezen.