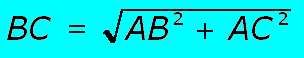|
Wat we hier gaan zien is een rechtsreeks gevolg van het gedrag van condensatoren of spoelen, onderhevig aan wisselstroom. |
|
|
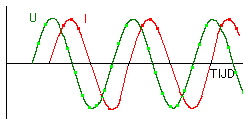
We zullen snel ondervinden dat in onze schakelingen de stroom niet steeds “in fase” met de spanning is. “In fase” beduidt dat in de tijd er GEEN verschuiving te zien is. Een beeld van de signalen met behulp van een oscilloscoop kan dit verduidelijken.
|
 |
|
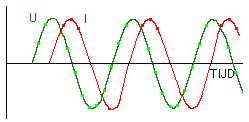
We hebben hier de spanning een groen, en de stroom een rood kleurtje gegeven. |
Met enige aandacht merken we dat de spanning eerder in de tijd start dan de stroom. Tevens hebben we gezien dat we in deze figuur de tijd onder de vorm van een hoekverschuiving kunnen voorstellen. (één volledige cyclus is 360°). |
|
Hoe kunnen we nu dit fazeverschil voorstellen ? |
|||||||||||
|
Vrij eenvoudig, bekijken we de figuur rechts: |
 |
||||||||||
|
Even je aandacht: we zien een rode vector die een bepaalde grootheid voorstelt (de spanning). De blauwe vector stelt de stroom (een tweede grootheid) voor. Tussen beide vectoren merken we een hoek van 90° op. Aangezien in deze toepassing de draairichting tegen de zin van het uurwerk loopt, kunnen we besluiten dat de spanning voorijlt op de stroom, of de stroom naijlt op de spanning en dit met 90°. |
|||||||||||
|
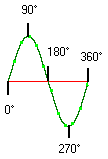
In één cyclus brengen we de bijzonderste hoekwaarden onder : Zie de fig rechts. Tevens stellen we de overeenstemmende hoek/radiaal waarden voor.
|
 |
||||||||||
|
|
|||||||||||
|
Verder … |
|||||||||||
|
Denken we ons het volgend probleem in : |
Alweer zal de driehoeksmeetkunde ons de oplossing leveren. |
||||||||||
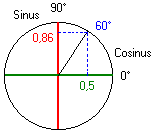 |
Ga even terug in je geheugen en je zal de figuur links herkennen die hopelijk een en ander wat verduidelijkt. |
||||||||||
|
Rechts zetten we het resultaat, wetende dat: (letters werden toegevoegd). a is de hoek tussen H en A Merk tevens de hoek van 90° tussen de segmenten A en O. |
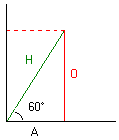 |
||||||||||
|
Wat halen we hier verder uit ? |
|||||||||||
|
Een voorbeeld zal helpen. Volgt de verschillende uitdrukkingen : |
driehoeksmeting leert ons : |
||||||||||
|
en nu met cijfers : |
Uit wat vooraf ging |
||||||||||
|
Denk er aan dat: |
de som van de hoeken van een driehoek gelijk is aan: 180° |
||||||||||
|
|
|||||||||||
|
|
|||||||||||
|
Iedereen is er van overtuigd dat deze man een zeer belangrijke bijdrage aan onze studie levert. |
Hij zal het nooit vermoed hebben, maar dank zij hem zijn we in staat om onze antennemast min of meer recht te zetten ! |
||||||||||
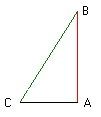 |
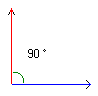
De figuur hier naast vertelt ons: We zien een rechte hoek (90°) in de driehoek. Tevens twee andere hoeken die noodzakelijkerwijs kleiner dan 90° zijn (de som van de hoeken in een driehoek is 180°) |
||||||||||
|
Het theorema van PYTHAGORAS stelt dat: in een rechthoekige driehoek het kwadraat van de hypotenusa gelijk is aan de som van de kwadraten van de twee andere zijden. Met andere woorden, in een driehoek AB en C de hoek A 90 ° bedraagt (een rechte hoek) dan is BC2 = AB2 + AC2 |
|||||||||||
|
Te onthouden : |
|||||||||||
|
Ons allen bekend: |
|
||||||||||
|
|
|||||||||||
|
|
|||||||||||
|
Eenmaal deze begrippen goed gekend zijn, is de rest van de studie wat gemakelijker te volgen. Gedenk PYTAGORAS !!!. |
|||||||||||