Capacitieve reactantie

Waar gaat dit nu weer om ?

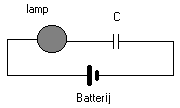
Wat een condensator is hebben we in een vorig hoofdstuk gezien bij de studie van de gelijkspanning. Ook het gedrag bij wisselspanning is bekend. Ter herinnering: een condensator, eenmaal opgeladen laat geen gelijkstroom door. Voor wisselstroom zagen we dat de frequentie van het signaal een belangrijke rol speelt. Hoe hoger de frequentie, hoe meer van de blokgolf er door ging. Herinner je het schema hiernaast.

Je weet dat de lamp NIET oplicht ( afgezien van een korte glimp). Iets blokkeert dus de gelijkstroom.

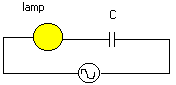
Vervangen we de gelijkstroombron door een wisselstroom. Verbazend, maar de lamp gloeit op.

Dit oplichten heeft duidelijk iets met de condensator te maken.

We gaan nog wat verder :

Verbazend, maar naargelang de frequentie vergroot zal de lamp feller gaan oplichten. De oorzaak hiervan is het bestaan, zoals bij de weerstand van een reactantie van de condensator met dit verschil dat zijn “weerstand” tegen wisselstroom daalt bij stijgende frequentie.

De reactantie is de eigenschap om zich tegen de stroom te verzetten en wordt als volgt uitgedrukt:

De reactantie schrijven we als X en drukken we uit in Ω

Met X in Ω
C in Farads
&#969 = 2 &#960 f
f in Hertz

Een voorbeeld :

We wensen de reactantie van een condensator van 100 pF bij een frequentie van 50 MHz te kennen.

O ja , nog dit: de condensator warmt niet op als er een stroom doorvloeit. (raar toch ??)

Wetend dat X = 1/C &#969
vinden we :
                                1
X =  __________________________
         100 10-12 x 2 x P x 50 106

                      1
X =   ______________________  = 31,8 Ω
               100 x2 x P x 50 10-6

Merk in de formule nogmaals op dat bij stijgende frequentie w de reactantie daalt.

Parameter staat in de noemer !

Het spreekt voor zich dat een grotere condensator een kleinere reactantie heeft (ook uit de formule).

De tabel hiernaast verduidelijkt de invloed van de frequentie op de reactantie van een condensator in ons voorbeeld van 10 pF. ( 10.10-12 F).

Je kan dit ook uittekenen onder de vorm van een grafiek (een prima oefening !)

De waarde van de reactantie is één ding, maar er is meer.

Het gaat om het effect van de faseverschuiving onder invloed van de frequentie en naargelang de keuze van condensator.

Bedenk dat ook bij gelijkstroom er op het allereerste moment een laadstroom loopt naargelang de grootte van de condensator. Een eventuele weerstand in serie beperkt de stroom en vertraagt het laadeffect.

Bij wisselstroom wordt de polariteit na een halve periode omgekeerd en ontladen we eerst, om daarna verder volgens deze polariteit op te laden.

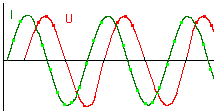
De condensator wordt in elk geval met enige vertraging opgeladen en ontladen. Er zal eerst stroom voeien en pas daarna zal de spanning op de condensator te zien zijn.

De vertraging van deze spanning op de stroom is 90 °.

Bekijken we de zaak met behulp van een oscilloscoop dan hebben we volgend resultaat:
In groen, de sroom
In rood, de spanning

Vectorïeel voorgesteld :

Zie de figuur rechts:

Tot slot :

De stroom die in fase met de spanning zou bestaan zou tevens oorzaak van vermogen zijn. In dit geval is deze nul en als product met de spanning over de condensator, een zeker I x r als vermogen geven. Er vloeit maar één stroom.

Een condensator verbruikt geen stroom (warmt niet op).

Te onthouden :

– de defasering van &#960/2 (90) van de spanning op de stroom. (Spanning ijlt na op de stroom)