|
Je voelt het al aan, door de nu bekende basiselementen te combineren kunnen we schakelingen met specifieke eigenschappen gaan bouwen. Als eerste bekijken we de seriekring. |
|
|
De zuivere seriekring : |
|
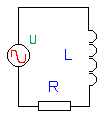 |
Links zie je de samenstelling: een wisselstroombron met frequentie f is serie geschakeld met een spoel L en een weerstand R. |
|
Wat kunnen we in deze kring opmerken ? |
|
|
Het is evident dat er een stroom zal vloeien. Over de klemmen van de elementen ontstaat een spanningsval ( Wet van Ohm ), zodat een bepaald vermogen zal verbruikt worden. |
Maar er is meer: Gezien de aanwezigheid van wisselstroom en reactantie zal er een faseverschuiving ontstaan tussen stroom en spanning. |
|
Verdiepen we ons even in deze zaak : |
|
|
Het is bekend dat de stroom I gelijk is aan het quotiënt van de spanning en de impedantie. Het lijkt dan ook logisch om de impedantie Z te bepalen. Maar Xl en R staan nu eenmaak 90 ° verschoven en dat maakt een puur algebraïsche benadering onmogelijk. De zaak moet vectoriëel bekeken worden. We maken dan ook gebruik van de stelling van Pythagoras. |
Aangezien we met een seriekring te maken hebben is de stroom het gemeenschappelijk element van dit soort kring ( de stroom door één component is gelijk aan die door de andere). Deze stroom zal daarom als de referentie gelden. Op deze as gaan we alle andere elementen van onze kring aanbrengen. ( rekening houdend met verschuivingen ). |
|
Voor de weerstand is de spanningsval gelijk aan R x I. |
Laat je niet misleiden. Wat voor gelijkstroom bestaat, bestaat ook voor wisselstroom. Je moet er wel aan denken dat voor reactanties ook de zin en richting van de vector van belang is. |
|
|
|
|
We beschikken nu over alle elementen om verder te rekenen : |
|
|
De spoel L, de weerstand R en de stroom zijn bekend. De formule L w I stelt de spanning over de klemmen van de spoel voor. Op een zelfde manier wordt de spanning R I berekend of de spanning over de weerstand. Wetende dat de spanning over L 90 ° verschoven ligt moeten we deze vector dan ook zo tekenen. Omdat de som van deze spanningen gelijk moet zijn aan de aangelegde U stelt de U vector de aangelegde spanning voor (vectoriële som). |
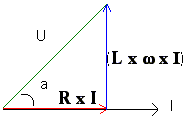 |
|
Deze U vector stelt dus de door de generator aangelegde spanning voor. Denk er aan dat je de spanning over beide elementen niet zomaar mag optellen. Je telt die meetkundig of vectoriëel op. |
De hoek”a” stelt de defasering tussen de stroom en de aangelegde spanning voor. Aangezien de kring een spoelgedrag vertoont, ijlt de stroom na op de spanning. |
|
|
|
|
Met formules : |
|
Gebruiken we hiervoor Pythagoras: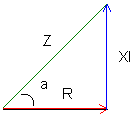 |
In het vectorschema hierboven stellen we vast dat de stroom gemeenschappelijk is. Eenvoudig Pythagoras toepassen hierop: |
|
Z2 = R2 + X2
( wie kan nog de vierkantswortel berekenen ??) |
met X = L ω |
|
Doen we dezelfde oefening nu met een condensator : |
|
|
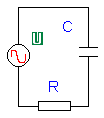
Eigenlijk is er niet veel verschil met het vorige. De condensator vervangt de spoel, je houdt nu enkel rekening met de gewijzigde fase ( tegengesteld ).
|
 |
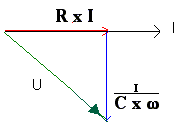 |
RI de spanningsval over R, I/Cω is de spanning over de klemmen van de condensator, U is de spanning die de generator levert. Voor het overige is de gedachtengang identiek. De impedantie van de kring: |
|
Z2 = R2 + X2 |
met X = 1/c ω |
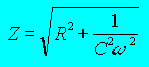 |
|
|
Tot slot : |
|
|
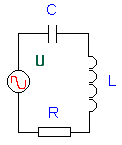
Als we nu een weerstand R, een condensator C en een spoel L in serie plaatsen, komen we tot de fameuze RLC kring. Het schema: |
 |
|
Wat betekent dit ? : |
|
|
Het gedrag van spoel en condensator zijn tegengesteld ( bij veranderende frequentie zal de waarde van de één vergroten de andere verkleinen, de fase is tegengesteld). Je kan dan ook stellen dat op één bepaald moment (frequentie) de invloed van de spoel door de condensator opgeheven wordt. |
|
|
Grafisch voorgesteld : |
|
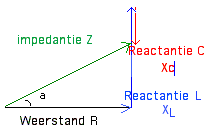 |
Inderdaad, de reactanties moeten van elkaar afgetrokken worden. Op de tekening is dat vrij duidelijk. Aan het einde van de grootste vector tekenen we de tweede, dat geeft dan het uiteindelijk resultaat. Als beiden gelijk zijn, is het resultaat ook NUL. |
|
|
UL Is de spanning op de klemmen van de spoel |
|
Noot : |
Als bij een gegeven frequentie de reactantie van de condensator groter is dan de reactantie van de spoel dan is het gedrag van de kring capacitief: de spanning zal in vertraging op de stroom zijn. Ook deze hoek wordt bepaald als φ. |
|
De formule die dit samenvat : |
|
|
Als je er rekening mee houdt dat de reactanties vectoriëel dienen verwerkt, kan je de bovenvermelde formule herformuleren. Let op: Pythagoras blijft ook hier gelden. |
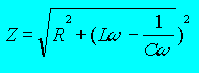 |
|
Eenvoudig, niet ? Dit toont gewoon dat beide reactantie van elkaar worden afgetrokken. |
Anders uitgedrukt : |
|
Een voorbeeld kan nuttig zijn : |
|
|
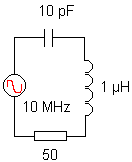
Stel dat we het voorbeeld hiernaast hebben. Wat is de impedantie van deze kring ? |
 |
|
Vervangen we in wat vooraf ging, de letters door de gepaste cijfers. |
XL = L ω = 1.10-6 x 2 x π x 10.106 |
|
Nu kunnen we de grafische methode verder uitwerken. We tellen beide waarden op maar rekening houdend met de zin (dus het verschil maken). We kunnen nu vaststellen dat de kring op deze frequentie van 10 MHz duidelijk een capacitief gedrag vertoont. De stroom ijlt dus voor op de spanning. |
Z = wortel ( 502 + ( 63 – 1592)2) |
|
Nog een voorbeeld . |
Stel dat de voeding nu 100 Volt bij 10 MHz bedraagt. |
|
U |
100 |
|
Spanning op de klemmen van de condensator |
|
|
De spanning op de klemmen van de spoel: |
|
|
De spanning op de klemmn van de weerstand: |
|
|
Merk dat Uc nu zelfs 103,5 V is, maar ook dat om de berekening sluitend te houden, de geometrische som (Pythagoras) moet gemaakt worden. |
|
|
Tot slot ! |
|
|
We hebben grootte van de defasering tussen be aangelegde spanning en de stroom nog niet bekeken. |
Hoe gaan we te werk ? |
 |
Hernemen we het diagram. |
|
Eens deze tangenswaarde bekend kan met een rekentoestelleje de hoekwaarde bepaald worden. |
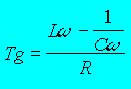 |
|
Oef, niet meer zo eenvoudig, maar niet minder belangrijk. Als je dit hoofdstuk goed begrepen hebt, zal het volgende zeker wat gemakkelijker zijn ! |
|

