In wat vooraf ging hebben we gezien dat de stroom in één enkele richting, volgens een conventionele zin, van plus naar min vloeit. De spanningsval over een weerstand rekenen we ook van plus naar min.
Bij de studie van wisselstroom is enige kennis van driehoeksmeetkunde nodig. Dit is wat we hier nu eerst gaan zien. Voor sommigen is dit nieuw, anderen moeten misschien enkel de stof wat opfrissen; in elk geval is het niet zo moeilijk.
Noties: Cosinus.
Net zoals de functie “product” = A x B, zijn sinus en cosinus eveneens functies (bewerkingen). Enig ruimtelijk inzicht verduidelijkt dit:
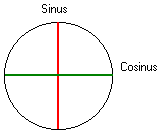
Hiernaast werd een cirkel met straal “r” getekend. We kennen aan de waarde r steeds de éénheid toe (1 of één).
De as in het groen is de cosinus-as.
De as in het rood is de sinus-as.
Wat moeten we hier nu mee beginnen ?
We gaan proberen om de sinus en cosinus van een hoek van 60° bepalen.
Grafisch is dit niet moeilijk. De cirkel heeft een straal van 1 (één). Daar tekenen, zoals op de figuur rechts te zien, een hoek van 60 ° op. Vervolgens projecteren we op beide assen, cos en sin, het snijpunt, lijn van de hoek en de cirkel. Als r = 1 dan is de sin = 0,86 en de cos = 0,5.
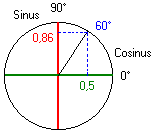
Sin (60°) = 0,86
Cos (60°) = 0,5
Tot wat dient dit allemaal ?
Eén toepassing is vlug gevonden als we er aan denken onze antennenmast op te stellen. Hiermee kunnen we immers de lengten van de spankabels berekenen ( maar denk toch maar aan wat reserve !).
Gaan we terug naar de functie f(x) = 2x. Wat betekent dit ?
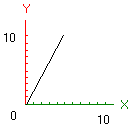
We laten gewoon de waarde X veranderen en bepalen de overeenstemmende waarde f(x) of Y. We krijgen dan : (zie hiernaast)
x = 1 2 3 4 5
f(x)= 2 4 6 8 10
Als je dit hebt begrepen, tekenen we de bijpassende grafiek van f(x). (De X- en de Y-waarden).
Om te begrijpen wat wisselstroom is gaan we terug naar wat we reeds bij het elektromagnetisme hebben gezien (opwekken van spanning).
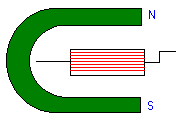
We maken zoals in de figuur rechts een soort generator : een spoel met hendel is tussen twee polen van een magneet geplaatst.
We sluiten de twee draden van de spoel op een oscilloscoop aan en draaien zo soepel mogelijk aan de slinger.
Op de figuur hieronder zie je hoe de generator spanning opwekt ( je ziet een punt zich volgens het lichtgroene patroon verplaatsen). Hoe de spanning in de spoel ontstaat, leggen we verder uit in het deel elektromagnetisme.
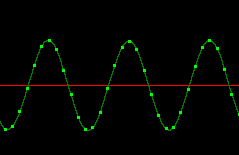
Toch een paar woorden uitleg:
Φ = B S N
Let op, de flux blijft NIET constant aangezien de spoel draait. De relatieve diameter verandert volgens de hoek waaronder ze zich te opzichte van het permanent veld bevindt. De hoeksnelheid wordt uitgedrukt als zijnde α = ω t.
De veldsterkte wordt dus :
Φ = B S N cos ( ω t)
We weten dat elke verandering doorheen een spoel een EMK of spanning opwekt die noodzakelijk deze uitdrukking volgt:
u = um sin(ω t)
Maak je niet ongerust als je niet alles tot in de details doorhebt. Ga er van uit dat een bewegende spoel in een magnetisch veld, een spanning opwekt evenredig met de relatieve snelheid. Deze volgt een sinusfunctie. De opgewekte spanning is een open-klem spanning: EMK, maar bij belasting zal de EMK naargelang de inwendig weerstand, verkleinen en een bronspanning met lagere waarde zijn.
Te onthouden :
Deze golvende vorm van de spanning noemen we “sinusoidaal”.
u = um sin(ω t)
Later zullen we zien wat ω , de periode, frequentie … betekenen.
U in volt
Um in volt, is de maximale spanning of piek waarde.
ω = pulsatie = 2 π f in radialen/seconde
f = frequentie in Hertz
t = tijd in seconden.
Een radiaal is die hoek waarvoor lengte van de boog op de cirkel gelijk is aan de straal (1). Er zijn dus 2 π radialen in een volledige cirkelomtrek of 360 °.
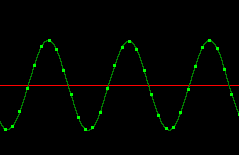
Hier rechts nogmaals een sinusoïdaal signaal :
Merk de rode lijn op die het geheel in twee delen verdeelt. We zien dat een even groot deel zich boven en onder deze lijn bevindt. Dit wijst op verandering van de richting van de stroom. Onder de rode lijn is de zin tegengesteld aan het deel erboven.
Hoewel het belangrijk is, hoef je toch niet te zwaar tillen aan wat hier uitgelegd werd. Tracht niet de formules uit het hoofd te leren maar onthou vooral het principe.

