De drie belangrijkste basisschakelingen van de transistor

In de elektronica hebben we nood aan verschillende soorten schakelingen.

Uit de studie van de generatoren voor gelijk- of wisselspanning weten we dat ze steeds een bepaalde inwendige weerstand hebben, waar we rekening mee moeten houden. Ze worden als Ri of Zi aangeduid (i staat voor inwendig). Als we een generator later volgen door een andere schakeling, hebben we er belang bij om de energie maximaal over te dragen. (PM Maximale energie-overdracht hebben we als belastingsweerstand en Ri gelijk zijn.)

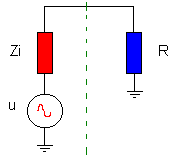
Bekijk de figuur rechts eens. De generator levert een wisselspanning U via een eigen (inwendige weerstand) Zi, aan een verbruiker (ontvangend element) R. (Deze ontvangende schakeling kan in ons vb de ingang van de transistorschakeling zijn).

Het is niet moeilijk te zien dat Zi en R een spanningsdeler vormen. Indien Zi zeer groot zou zijn, zou men over de belasting R bijna niets terugvinden. Bijna de volledige spanning U staat over de inwendige impedantie Zi. Denk er aan dat R ook de ingang van de transistorversterker is. Het komt er dus op aan de uitgangsimpedantie van de een kring aan te passen in functie van de ingangsimpedantie van de kring die er op volgt, of omgekeerd. In de transistortechniek bestaan er drie basisschakelingen met elk hun specifieke eigenschappen, ook op het vlak van in- en uitgangsimpedantie. We kiezen dan ��n van deze drie basisschakelingen naargelang de gewenste eigenschappen in de specifieke schakeling.

Maar eerst, terug naar de condensator :

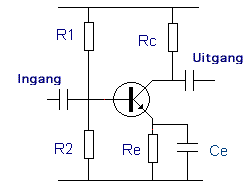
We hebben reeds het gebruik van de condensator bij de versterker gezien. We hadden dit element nodig om het signaal van of naar de transistor te voeren zonder de DC instelling te verstoren.

Maar we kunnen de condensator nog op een andere manier toepassen. We gaan via een condensator over de emitterweerstand, het AC deel naar massa laten vloeien. De AC-impedantie moet dus klein zijn, men noemt dit de ontkoppeling.

Gezien de wisselspanning zonder de condensator volgens de waarde van Re een vermindering van het ingangssignaal betekent, daalt de uiteindelijke versterking. Door de ontkoppeling door de condensator Ce gaat de versterking veel groter zijn.

De gemeenschappelijke emittorschakeling :

Voor AC ( wisselspanning ) staat door de lage impedantie van Ce, de emittor op niveau massaof nul.

Door het aanleggen van een wisselspanning aan de ingang, wordt deze bij de DC instelling gevoegd. Vbe doet bijgevolg Ic stijgen of dalen volgens dat Veb dit doet.

De spanningsval Rc x Ic volgt eveneens. Als Rc x Ic stijgt, zal de spanning Vce verminderen. Bij de volgende alternantie gebeurt het omgekeerde, dus, als Rc x Ic daalt, stijgt Vce .

Samengevat: een verhoging van de spanning aan de ingang heeft een daling van de spanning op de uitgang als gevolg. De verandering van spanning op de uitgang is ook vele malen groter dan deze op de ingang (versterking, weet je nog !). Er is dus zowel een verschil is fase als in amplitude.

Van waar komt die winst ?

Verandering van Ic als gevolg van r Ib doet er één over Rc ontstaan. Deze wordt via de condensator met voldoende grootte afgenomen ( het werkpunt wordt over de belastingslijn verschoven). De condensator heeft een zeer kleine impedantie, die zeker ten opzichte van de weerstand te verwaarlozen is. De stroomwinst komt uit de omzetting van de voedingsspanning naar een grotere collectorstroom.

Hoe kunnen we de winst bepalen ?

De winst wordt bepaald als de verhouding van de verandering van de uitgangsspanning tegenover de ingangsspanning en is dus onbenoemd (geen eenheidsmaat).

Het bestaan van weerstand r’e uit vorig hoofdstuk :

25
r’e = ______
Ie

met Ie in mA

Deze uitdrukking is zeer belangrijk. Het is de basis of sleutel voor de versterking.

Het teken “-” Wijst naar het omkeren van de fase op de uitgang ten opzichte de ingang.

Ingangsimpedantie van de transistor :

Zonder verder bewijs onthouden we:
met // = parallel
Zi = Z input (ingang)

Uitgangsimpedantie van de transistor :

Zonder verder bewijs onthouden we:
Zo = Z output (uitgang)

Een voorbeeld zal dit verduidelijken :

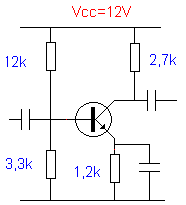
We houden ons niet met de waarden van de condensatoren bezig. Hun gedrag is als van een kortsluiting voor de frequentie van het ingangssignaal.

We berekenen de waarden van de versterking, en de in- en uitgangsimpedanties.

1 – We gaan de waarde van r’e berekenen. Daarvoor moeten we Ie kennen.
We berekenen eerste de spanning op de basis: Vb

3300
Vb = _____________ x 12 = 2,59V
3300 x 12000

2 – De spanning op de emittor Ve :

Ve = Vb – 0,7 = 1,89V

3 – We berekenen Ie

Ie = Ve/re 1,89/ 1200 = 1,57 mA

4 – Nu kunnen we r’e gaan bepalen:

25 25
r’e = _____ = _______ = 16 Ω
Ie 1,57

5 – En nu de versterking:

A = Rc/ r’e 2700/ 16 = 169

6 – We bepalen de ingangsimpedantie:

Zi = R1//R2 (bij benadering)
Zi = 2588 Ω

7 – 6 – We bepalen de uitgangsimpedantie:

Zo = Rc Zo = 2700 Ω

Samenvatting van de eigenschappen van de gemeenschappelijke emittorschakkeling:

– Grote winst
– Uitgang met 180 ° verschoven
– Grote ingangsimpedantie
– Grote uitgangsimpedantie

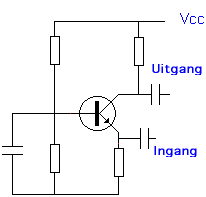
De gemeenschappelijke basis schakkeling :

Hiernaast zie je de schakeling, maar bemerk

Een paar veranderingen:

De basis ligt voor wisselspanning aan de gemeenschappelijke massa, door de condensator parallel op de weerstand.

Het ingangssignaal wordt aan de emitter gelegd. Voor de werking van de transistor is er geen verandering in die zin dat dit in de gesloten ingangskring op het zelfde neerkomt als wanneer het signaal aan de basis zou worden gelegd. De verandering van ingangsstroom is de oorzaak van een grote verandering van collectorstroom (zoals bij voorgaande schakeling).

Op het vlak van polarisatie is er niets nieuws daar dit nog steeds in de delerkring gebeurt.

Onze ingangsimpedantie :

We kunnen zonder meer aannemen dat:
We zien onmiddellijk dat deze klein is.

Onze uitgangsimpedantie :

Dus:
Zo = Z output (uit)

Onze transistor heeft een winst van :

We vermeldden het al, r’e heeft de waarde van :

25
r’e = ______
Ie

met Ie in mA

In dit geval is de uitgang in fase met de ingang.

Eigenschappen van de gemeenschappelijke basisschakeling:

– Grote winst
– Geen faseverschuiving
– Lage ingangsimpedantie
– Hoge uitgangsimpedantie

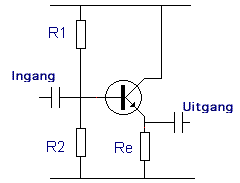
Gemeenschappelijke collectorschakeling of emittorvolger :

Je ziet onmiddellijk dat de collector via de voeding ( kleine inwendige weerstand ) aan massa ligt. De collector is daarom gemeenschappelijk. De polarisatie op de basis is klassiek ( met een spanningsdeler ).

Je merkt ook dat de emitter niet meer ontkoppeld wordt. Je kan aanvoelen dat de in- en uitgangssignalen zowat gelijk zullen zijn.

Het verschil zullen we vooral op het vlak van de impedantie zien: daarom gaat het hier eerder om een impedantieaanpassing ( IN / UIT).

De winst bij deze schakeling :

Het werd reeds aangehaald, de weerstand r’e heeft de waarde van :

25
r’e = ______
Ie

met Ie in mA

Met andere woorden: de spanningswinst van een gemeenschappelijke collectorschakeling is iets kleiner dan één (1).

De ingangsimpedantie :

We nemen aan dat :
De ingangsimpedantie wordt vooral bepaald door R1 en R2 .

De uitgangsimpedantie :

Ook hier zonder meer:
Zo = Z output (uit)

Rs//R1//R2
Zo = r’e + ____________
β

De karakteristieken van de gemeenschappelijke collectorschakkeling samengevat:

– Winst één
– Geen fazeverschuiving
– Hoge ingangsimpedantie
– Lage ingangsimpedantie

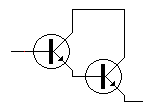
Een bijzondere toepassing van de gemeenschappelijke collectorschakkeling, de Darlington :

Dit is een frequent gebruikte schakeling met bijzondere eigenschappen. Deze schakeling ( zie rechts ) wordt veelvuldig in één enkele behuizing ondergebracht. Er komen dan zoals bij de normale transistor drie draden uit, zodat je uiterlijk geen verschil ziet. Deze schakeling is bekend als de DARLINGTON.

Uitvoering: de twee collectoren worden aan elkaar verbonden. De emittor van ��n ligt aan de basis van de eerste.

Deze schakeling heeft wel een bijzondere eigenschap, namelijk de zeer hoge stroomversterkingsfaktor

Tot nu toe hebben we de drie basisschakelingen op zichzelf bekeken. Met zo een basisschakeling zijn we niet veel vooruit: we moeten ze met andere kringen samenbouwen tot grotere schakelingen. Je voelt al aan dat we hierbij rekening moeten houden met andere aspecten. Door dit inpassen in een grotere schakeling zullen we immers de voorgaande kringen belasten, en achterliggende kringen gaan op hun beurt onze transistortrap belasten.

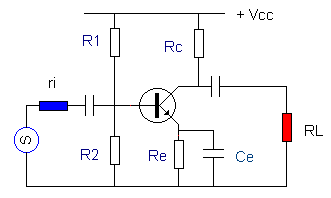
Laten we het niet te ingewikkeld maken en deze be�nvloeding enkel bij de gemeenschappelijke emitterschakeling wat uitdiepen. Wat gebeurt er met de DC- en AC-stromen door deze effecten ?

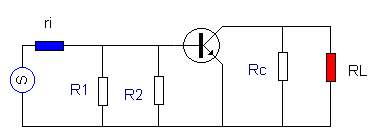
We vervolledigen de basisschakeling met een stroomgenerator, met een eigen weerstand ri aan de ingang en een belasting RL aan de uitgang. In RL staat de “L” voor LOAD.

Vereenvoudigen is de boodschap – dat gaan we dus ook doen:

Voor de gelijkstroom passen we toe:

1 – Kortsluiten van de stroombron van wisselstroom

2 – Wegnemen van de condensatoren.

Met hetgeen nu overblijft kunnen we de gelijkstroom en spanningen in deze schakeling berekenen.

Voor de wisselstroom passen we toe :

1 – Kortsluiten van de spanningsbron en stroombron aansluiten.

2 – Kortsluiten door de condensatoren.

Dit is het resultaat. Wat uitleg ?
De spanningsbron (kortsluiten voor AC) brengt R1 parallel aan R2, en Rc wordt aan de massa gekoppeld om dezelfde reden.

Door de kortsluiting van de condensatoren plaatsen we RL parallel aan Rc.
Het kortsluiten van C over de emittorweerstand brengt deze aan de massa.

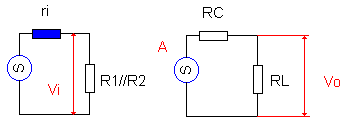
Hertekenen van de versterker:

De tekening aan de linkerkant stelt de ingang kant voor. Een spanningsbron met inwendige weerstand ri wordt belast met een weerstand samengesteld door R1 en R2 in parallel. We hebben een klassieke spanningsdeler. De ingangsspanning die wordt versterkt is enkel Vi.

Aan de rechterkant zien we de kring vanuit de collector. Een spanningsbron (A x Vi) wordt aan een spanningsdeler gelegd bestaande uit de collector weerstand RC en de belasting RL, wat ons Vo oplevert.

Je ziet dat de versterking (A) alleen niet volstaat om het gedrag van deze versterkingstrap te bepalen. Een goed deel van de spanning gaat verloren door invloed van de inwendige weerstanden van de andere kringen.

Tot zover dit toch niet eenvoudige hoofdstuk. Voor ons volstaat het te weten dat er drie basisschakelingen bestaan met elk hun specifieke eigenschappen. De gemeenschappelijke emittorschakeling wordt het meest gebruikt.