Inductieve reactantie

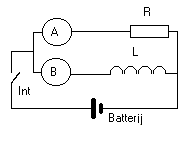
Het begrip inductantie hebben we reeds ontmoet bij de studie van gelijkstroom en elektromagnetisme. Ook hebben we al wat over zelfinductie gezien.

Bekijken we het schema hiernaast (reeds gezien). We stelden vast dat de lamp slechts na enig vertraging aanging bij het sluiten van de schakelaar, en ook na het weer openen pas na een tijdje weer doofde. Deze proef illustreert het effect van zelfinductie.

Een paar eenvoudige dingen bij het schakelen van spoelen :

Bij het plaatsen van ( L1, L2, L3), inductanties in serie stellen we vast dat:

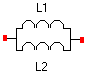
Bij het plaatsen van inductanties ( L1, L2), in parallel wordt het resultaat:

De coëfficient van zelfinductie wordt als L genoteerd, de eenheid wordt in Henry uitgedrukt.

Hoe zal de spoel zich bij wisselstroom gedragen ?

Zoals bij de condensator, zal het gedrag van de spoel frequentieafhankelijk zijn. Deze afhankelijkheid heet de reactantie.

De reactantie van de spoel is de eigenschap waarmee de spoel zich tegen wisselstroom verzet.

De reactantie X wordt in Ω uitgedrukt.

Waarin X in Ω
L in Henry (symbool : H)
&#969 = 2 &#960 f
f in Hertz

Een voorbeeld van berekening :

We beschikken over een spoel van 10 µH en wensen de reactantie bij een frequentie van het signaal van 50 MHz te kennen.

Wetende dat X = L &#969
en vinden we :
X = 10 10-6  x 2 x &#960 x 50 106
X = 3140 Ω

In tegenstelling tot de condensator stellen we vast dat de reactantie van een spoel stijgt bij stijgende frequentie.

Natuurlijk is de reactatie groter als een grotere spoel wordt gebruikt (zelfinductie L).

De tabel rechts zal je wel overtuigen. Als oefening is het wel eens nuttig om deze cijfers op een grafiek uit te zetten. Een spoel van 10 µH wordt bij meerdere frequenties uitgerekend.

Vergelijk nu deze spoel met een condensator:

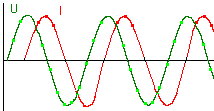
Zoals bij de condensator zal ook de spoel een verschuiving in tijd tussen stroom en spanning veroorzaken. Ook nu kunnen we verwachten dat het gedrag tegengesteld zal zijn.

De condensator vertraagt de spanning op de stroom ( men zegt ook: de stroom ijlt VOOR ). Bij een spoel is het omgekeerd. De spoel vertraagt de stroom op de spanning ( men zegt ook: de stroom ijlt NA).

Herhalen we vanaf het begin. De spoel vertraagt de ontsteking van de lamp, en omgekeerd bij het doven. Zou het dan niet logisch zijn als we stellen dat de spoel energie opslaat ( in het magnetisch veld ) en bijgevolg op het moment nul als er nog geen energie voor de lamp beschikbaar is. Bij het doven zal de energie in dat magnetisch veld oorzaak zijn dat het lampje niet onmiddellijk dooft: het blijft branden tot uitputting van de magnetische energie in het veld.

Als we de zaak bij middel van een oscilloscoop onderzoeken kunnen we het gedrag van stroom en spanning goed volgen.
in groen de spanning
in rood lde stroom

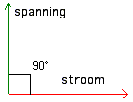
Vectorïele voorstelling : (klinkt intelligent)

Onthou dat de spoel een faseverschuiving van 90 ° veroorzaakt met andere woorden P/2 in radialen uitgedrukt. De stroom ijlt NA !!

Een perfecte spoel (zonder enige weerstand) verbruikt geen vermogen (cfr. de condensator ).De componenten van stroom in fase met de spanning over de condensator is NUL.

Natuurlijk is de reactantie van de spoel evenredig met zijn coëfficiënt van zelfinductie (grootte).

Met deze kennis kunnen we nu wat fundamenteler op de zaken ingaan.