Niet-sinusoidale signalen

We leren alle dagen bij. Tot nu leerden we over gelijkstroom en sinusoïdale signalen. Niet alle signalen hebben deze vorm. Je voelt wel aan dat ook hier een groot verschil bestaat, vooral wat betreft vermogens enz.

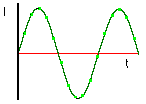
Als we beide hoger getoonde vormen vergelijken zien we duidelijk dat ze niets met elkaar gemeen hebben (of toch). Een groot man, FOURRIER, heeft wiskundig aangetoond dat elk “periodiek” signaal kan ontbonden worden in een aantal sinusoïdale signalen. Deze signalen staan in frequentie en amplitude in verhouding met elkaar volgens de vorm van het periodiek signaal. De samenstellende signalen noemt men harmonischen van de basisgolfvorm.

Harmonischen bestaan niet alleen in de elektronica, maar dat zien we later nog wel.

Definitie :

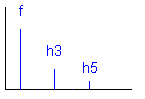
Een harmonische is een geheel veelvoud in frequentie van een signaal met een bepaalde f.

De tweede harmonische is dit signaal bij tweemaal de frequentie of 2 f , de n-de harmonische , n f.

Harmonischen in de natuur .

Waarom horen we een noot “sol” op een piano niet hetzelfde als de zelfde “sol” op een viool ? De aanwezige harmonischen liggen hier aan de basis.

De basisfrequentie is voor beide instrumenten dezelfde maar de verdeling van de harmonischen ligt totaal anders.

Hetzelfde ondervinden we met onze stem. Dank zij die samenstelling van harmonischen kunnen we ook goed stemmen van mensen herkennen. Maar keren we terug naar de radio.

We gaan door: Voor een beter begrip is het nodig te weten hoe een periodiek, niet- sinusvormig signaal ontrafeld wordt tot harmonischen die op een bepaalde manier met elkaar verband houden.

Een sinusoidaal periodiek signaal wordt als volgt voorgesteld:

Daarin staat Am voor de maximum- of piekwaarde, w = 2 p f als pulsatie en Φ de faze.

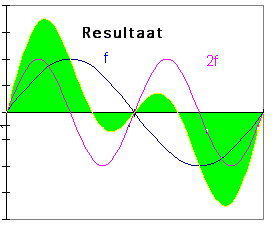
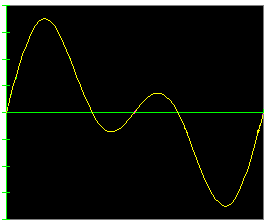
Hoewel niet eenvoudig, is het mogelijk om meer dan één sinusgenerator in serie te plaatsen. We laten er één een signaal met frequentie f leveren, en de andere met 2f. Zie de figuur hiernaast. We zien dat beide signalen dezelfde amplitude hebben en geen verschuiving.

Op de grafiek zien we het blauwe signaal met frequentie f en het violette met 2 maal deze f. Beide samengesteld levert de groene grafiek van f + 2f.

Fourier heeft dit tot wiskundige formules herleid.

De grafische redenering zal voor de meesten wel het gemakkelijkst uitvallen. Per tijdsmoment tellen we de vectoren op. De polariteit is daarom functie van de relatieve grootte op dat moment.

Waarom worden de harmonischen besproken ?

In de natuur, maar zeker ook in de radio-elektriciteit, komt dit fenomeen veel voor. Het volgende zal je wel overtuigen.

Stel:

We beschikken over een oscillator (generator) op 10 MHz. Toch moeten we om een bepaalde reden beschikken over 30 MHz. Dit is eenvoudig:

Het volstaat deze 10 MHz door een niet-lineair element ( versterker , diode…) te voeren en we creëren naast de fundamentele frequentie een hoop andere signalen. Door bv. een filter is het dan mogelijk ons gewenste 3f-signaal te isoleren en desnoods voort te versterken voor gebruik. Erg simpel (in theorie) !

Stel dat je onzorgvuldig bent:

Je zender op 50 MHz stoort de omroep en je buurman is niet tevreden. Gevolg: geklaag, maar er bestaat een oplossing:

Het is zo goed als zeker dat de 2e harmonische 2f of 50 x 2 = 100 MHz als verantwoordelijke moet gezien worden. Een filter kan je zendsignaal zodanig zuiveren dat GEEN 100 MHz-signaal meer voorkomt.

Je hebt als hobby-man je ontvanger zelf gebouwd. Maar bij de eerste test stel je vast dat je ook andere signalen hoort, op frequenties waarvoor je ontvanger niet werd gebouwd. Wat is er aan de hand ?

De harmonischen van de oscillator van je ontvanger ( nodig voor de ontvangst , zie later ) kunnen, gecombineerd met andere ontvangen signalen ( zelfs buiten de band ), nog een vergelijkbaar signaal leveren dat bij menging nadien hoorbaar wordt. ( details bij de studie van de ontvanger )

Knutselaar zoals je bent, heb je een digitaal uurwerk gebouwd en in je station geplaatst. Sindsdien hoor je een veelvoud van niet- gemoduleerde stoorsignalen. Wat gaat er nu weer mis ?

Je klok werkt op basis van een kwartskristal en produceert vierkantgolven. Verder wordt alles digitaal ( met vierkantgolven ) bewerkt. Die vormen echter een groot aantal harmonische producten die je ontvangst storen. Remedie: de klok buiten of in een goed afgeschermde omgeving zetten.

Let op: computers kunnen ( en zullen ! ) dikwijls kopzorgen opleveren. Een goed afgeschermde computer is onontbeerlijk. Meestal gaan prijs en kwaliteit hier samen.

We kunnen nog een groot aantal dergelijke voorbeelden geven, we haalden ze enkel aan om het belang te onderstrepen. We zullen nu het spectraal aspect zien.
Tot nu werd enkel de amplitude onderzocht door met een oscilloscoop het signaal te bekijken. De amplitude werd in functie van de tijd nagegaan.

Hiernaast zien we een verandering van amplitude in functie van de tijd. De tijd volgt de X-as en de stroom verloopt volgens de Y-as.
Laten we nu eens in plaats van de tijd, de frequentie uitzetten. Wat kunnen we hieruit leren?

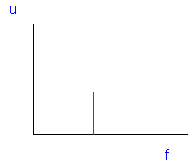
Ging dit niet snel? Op de X-as zien we de frequentie uitgezet. Op de Y-as staat nog steeds de amplitude zoals op de oscilloscoop. Door werkwijze kunnen we de amplitude meten volgens de aanwezige frequentie(s). Het toestel waarmee we dit kunnen meten is een “spectrum-analyser” . Je voert immers een spectrale analyse uit. Ons voorbeeld is simplistisch en niet echt het meten op deze manier waard. Merk ook op dat we de vorm van het aangelegde signaal nu niet meer zien.

Met een samenstelling van meer dan één signaal wordt het echter meer zinvol.

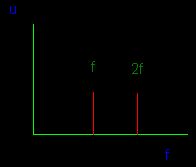
Links onder zien we het resultaat van twee sinussignalen in serie zoals hierboven. Aan de rechterkant zien we datzelfde signaal via een spectrumanalyser. Het rechtersignaal wordt op de analyser duidelijk als twee signalen getoond.

Een spectrumanalyzer is de droom van heel wat radioamateurs, maar zo’n toestel is zeer duur.

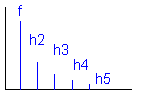
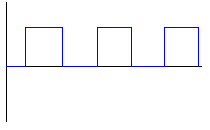
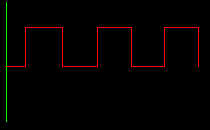
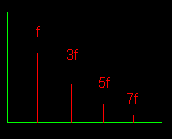
Leggen we een vierkantsgolf aan dan zien we rechtsonder het resultaat op spectraal vlak. Tot de zevende harmonische is in dit voorbeeld te zien.

Merk intussen op dat er enkel ONEVEN harmonischen te zien zijn. De even bestaan niet ! De verklaring volgt hieonder:

Niet verwonderlijk maar er bestaat een verband tussen de vorm van het aangelegd signaal en de samenstellend frequenties :

We stelden vast dat een vierkantsgolf enkel oneven samenstellende golfvormen bezit. Hoe kunnen we nu zien hoe de spectrale verdeling in functie van de golfvorm verdeeld wordt?

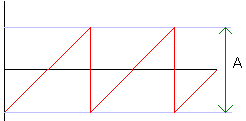
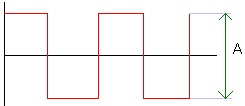
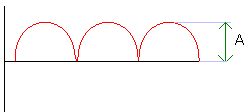
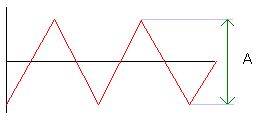
We produceren vier fundamentele of basisgolfvormen met rechts hun spectrale samenstelling.
In de formules staat “n” voor de rangorde van de harmonische.
Nemen we als voorbeeld het eerste signaal en bepalen we de amplitude van de 3e rangorde van harmonische. Stel dat het basissignaal 10 V bedraagt.
10

2A
V_n= ___
n π

       4A   1
V_n= __ _____
      π    4 n²-1

4A
V_n= ______
( π n)²

Hoe kunnen we nu weten of een signaal harmonischen bevat en welke ?

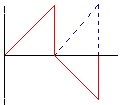
Neem maar aan dat, als een signaal halvegolf-symmetrisch is, er oneven harmonischen zijn.

Echt duidelijk is dit wellicht niet. Een voorbeeld kan de mist laten optrekken: kijk hiernaast naar de rode golfvorm. Nemen we nu de symmetrie van de negatieve alternantie in gestippeld blauw. Vervolgens laten we dit naar links verschuiven en merken we dat deze gestippelde vorm exact de positieve alternantie is. Hieruit mogen we de conclusie trekken dat er GEEN even harmonischen zijn.

Stoppen maar. Het volgende hoofdstuk gaat over de transformator. Daarrmee hebben we dan de wisselstroom volledig behandeld.