De polarisatie van transistoren

Transistors moeten gepolariseerd of ingesteld worden al naargelang het gewenst doel. Hoewel het principe eenvoudig is, is dit in de praktijk toch dikwijls een bron van frustratie bij het ontwerpen van kringen.

De noodzaak om te polariseren :

1 – De transistor MOET gepolariseerd worden, zoveel is zeker. We moeten op de aansluitingen (één of twee) een bepaalde spanning aanleggen om de transistor naar wens te laten functioneren. Polariseren gebeurt door het aanleggen van een gelijkspanning die voldoet aan bepaalde criteria. Deze criteria hangen af van wat we met de transistor willen doen. Je begrijpt wel dat een toepassing als schakelaar andere eisen stelt dan een versterker voor kleine of grote signalen.

2 – Bij een versterker moet de polarisatie zo zijn dat we na de versterking van een zwakke wisselspanning op de ingang, we een signaal met precies dezelfde vorm aan de uitgang terugvinden. 180� faseverschuiving, of vergroting van het signaal, beschouwen we hier niet als een wijziging. We spreken hier van een lineaire versterking (Noteer: verzwakking kan men als een negatieve versterking zien, een versterking één (1) levert een identiek signaal op.)
Het instelpunt waarop we gaan werken, wordt bepaald door de spanning tussen emitteer en basis. Dit punt volgt de belastingslijn ( een punt verschuift op die lijn volgens dat verschil in spanning Vbe ). Bekijken we dit nu wat praktischer.

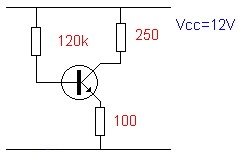
De eenvoudigste polarisatievorm : vaste polarisatie of basispolarisatie.

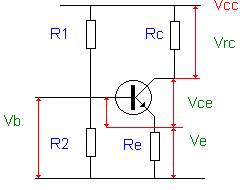
Laten we beginnen met te wennen aan de voorstelling zoals hiernaast.
De bovenste lijn noteren we als Vcc. De onderste lijn is de NUL lijn of de referentie of demassa lijn van NUL Volt.

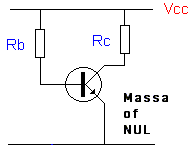
Bij dit type van polarisatie is het zo goed als uitgesloten om een stabiele instelling als versterker te verkrijgen. Zoals reeds opgemerkt zullen thermische effecten ( bijv. opwarming ) tot een verschuiving van de instelling leiden. β wordt hierdoor beïnvloed.. Het is duidelijk dat we hierdoor dit soort polarisatie zullen vinden wanneer de transistor als schakelaar wordt gebruikt.

Leggen we de basis aan massa dan is de basis/collector-overgang niet gepolariseerd en vloeit GEEN basisstroom met als gevolg GEEN collector- of emitorstroom. De transisor is gesperd en Vce is dezelfde als de voedingsspanning Vcc .

Stellen we de basis bij middel van de weerstand Rb ergens op een punt van de belastingslijn in, dan zal er door de junctie stroom vloeien volgens de waarde van Rb. Doen we dit zodanig dat de transistor in verzadiging treedt, dan wordt Vce quasi NUL Volt.

Tweede manier, door reactie van de emittor :

We kunnen het niet voldoende herhalen, maar de grootste moeilijkheid bij de instelling van een transistor in het lineair gedeelte van de belastingslijn, is de stroomversterkingsfaktor βdie varieert volgens de temperatuur. Een minimale stroomverandering als gevolg van temperatuur heeft bij grote versterking, ook grote gevolgen.

We benadrukken: een verandering van Ic als gevolg van de verandering van β door de temperatuur, laat het punt P verschuiven. Op het diagram van de collector merken we dit doordat Vce verkleint als gevolg van een grotere spanningsval over de collector- weerstand.

Het is belangrijk dit mechanisme ( vergroten of verkleinen tot het uiteindelijke resultaat ) goed te begrijpen. Dit soort gedachtengang zal nog voorkomen.

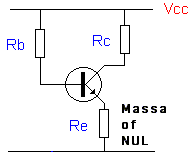
Er zou geen transistortoepassing bestaan als het niet mogelijk was om dit effect tegen te gaan. De gevolgen van verandering door temperatuur moet tegengegaan worden. Een weerstand in de emitorkring brengt de oplossing. Volg de gids:

Stel, in het schema links vergroot de IC om een of andere oorzaak (ook temperatuur). De stroom Ic (emitor) zijnde Ie = Ic + Ib zal eveneens vergroten. De spanningsval over Re zal volgen. VRe = Re * Ie.

We zien onmiddellijk dat hiermee de instelling van de basis veranderd wordt (spanning junctie basis/emitor).

Langs de kant van de basis is op het vlak van de spanning niets verandert . Maar als we de spanning tussen de emitor en massa bepalen, zullen we opmerken dat deze een weinig is gestegen. (VRe= Re * Ie). Het gevolg hiervan is, een daling van Vbe. Bij nader toezien is de stuurspanning gedaald met als onvermijdelijk gevolg, een daling van de stuurstroom Ib. Eenvoudig om hieruit te besluiten dat de collector stroom Ic in waarde daalt en natuurlijk ook de emittorstroom Ie. Dat is nu juist wat we wensten.

De omgekeerde werking, dalende temperatuur is eenvoudig te reconstrueren. Maak deze oefening eens ter controle.

Belangrijk :

We hebben nu de belangrijke rol van de emitorweerstand Re bestudeerd. Je zal deze aanpak in praktisch alle polarisatiemethoden terugvinden.

Over naar de praktijk :

Denk er aan dat Ic en Ie niet veel van elkaar verschillen. Immers Ib is zeer klein. We gaan IC berekenen.
We kunnen dan de volgende vergelijking opschrijven:

Vcc – ( Rc.Ic + Vce + Re.Ie) = 0 (Kirchoff weet je nog ?)
Bekijk goed het schema rechts en het wordt eenvoudig.

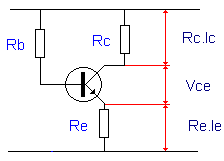
Na wat herschikken vinden we:

Vcc – Vce

Ic = ___________

Rc + Re

We gaan na wat dit op de belastingslijn geeft. Hiervoor gaan we terug naar de twee bijzondere punten: spertoestand (Ic zijnde NUL) en verzadiging (Vce zijnde zowat NUL voor Ic maximaal en enkel door Rc en Re beperkt). We vinden :

voor Ic=0 hebben we Vcc = Vce

voor Vce=0, Ic= Vcc/ Rc + Re. Hiermee kunnen we deze fameuze lijn tekenen: (zie hieronder)

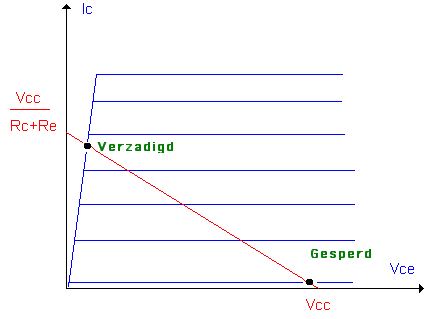
We hebben het over verzadigingsstroom van de transistor. Dit begrip moeten we goed inzien. Laten we de stroom Ic toenemen door het stijgen van Ib op de basis. We stellen dan een spanningsstijging over Re en Rc vast. Toch een eenvoudige toepassing van de wet van Ohm ?
(VRc = Rc.Ic et VRe = Re.Ie) om volledig te zijn, zie hiernaast.

Op een bepaald moment wordt Vce zowat gelijk aan NUL (verzadiging). De transistor kan dan niet nog meer stroom door de collector laten vloeien. Dit punt wordt verzadigings- puntgenoemd.

Hoe groot deze verzadigingsstroom zal zijn wordt niet door de transistor maar wel door uitwendige elementen Rc en Re bepaald. Deze waarden zijn van groot belang bij de berekening van de versterking van de transistor (zie later).

Bekijken we eens wat er aan de kant van de BASIS gebeurt :

We berekenen enkele spanningen aan de basiskant :

We kunnen schrijven (zie hiervoor het schema) :

Vcc – (Rb.Ib +Vbe + Re.Ie) = 0

Kirchoff in een gesloten kring… enz). Verder werd aangenomen dat Ic ongeveer gelijk aan Ie is, en dat b Ib = Ic

We schrijven dan:

Vcc – Vbe

Ic = _________

Re + (Rb/ β)
Hierdoor zien we dat de stroomwinst van de transistor β hier haar invloed laat gelden.

Voor- en nadeel van deze polarisatiemethode :

We beschikken nu al over een tamelijk goede stabilisatiemethode maar we weten dat transistors een grote spreiding van eigenschappen of parameters kunnen hebben. Een voorbeeld : een bekende transistor type BC 107 kan een stroomversterking hebben tussen pakweg 70 en 300.
Dit heeft als gevolg dat de schakeling die we hebben ontworpen, niet zonder meer nagebouwd kan worden. In het begin zal de schakeling perfect werken, maar bij gebruik van een vervangtransistor totaal niet meer funktioneren. Weg ons mooie vooruitzicht. Dit is dus nog niet de ideale schakeling.

Praktische toepassing :

Stel dat we een transistor hebben met β = 100.
Hoe groot is de stroom Ic ?
We passen de formules toe:
Vcc – Vbe
Ic = _________
Re + (Rb/β)
dit geeft ons :
12 – 0,7
Ic = _________________ = 8,7 mA
100 + (120000/100)

Bereken dit ook eens voor een β = 300

Een derde methode, de automatische polarisatie :

Deze werkwijze is economisch en wordt daarom veel en met goed gevolg toegepast.

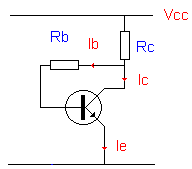
Wat nieuws ?
De basisweerstand Rb wordt NA Rc genomen .
Wat zal er nu gebeuren als β verandert ?
Stel β vergroot, hierdoor zal Ic vergroten. Als Ic vergroot zal de spanningsval Rc dit ook doen. Ic zal eveneens vergroten en gelijktijdig de spanning aan de klem van Rb (de voeding die via Rb de basisstroom levert wordt kleiner). Gevolg is duidelijk een verkleining van Ib wat weer als gevolg een daling van Ic heeft .

Een paar berekeningen volgens het schema aan de basiskant:
We kunnen schrijven :
Vcc – ( Rc (Ic+Ib) + Rb . Ib) =0
We weten dat Ic ongeveer gelijk aan Ie en dat β Ib = Ic is.
Hieruit volgt dat Ic =
Vcc – Vbe
Ic = _________
Re + (Rb/β)
We vinden dezelfde formule als bij voorgaande polarisatie. Veronderstel dat we Rc nul maken , de spanning tussen basis en emittor (massa) van de orde van de 0.6-0.7V, of spanning van de junctie Vbe. Het echt in verzadiging brengen van deze schakeling is niet mogelijk want Vce kan NIET ONDER 0.7 V dalen.

Om in dit voorbeeld ons werkingspunt in het midden van de belastingslijn te plaatsen passen we volgende relatie toe:

De stroom IC wordt bepaald door:

Voor- en nadeel van dit soort polarisatie :

Ons werkpunt is beter gestabiliseerd, maar we stellen vast dat de stroomwinst van de transistor nog steeds mee de regeling van de ruststroom bepaalt. Verzadiging wordt nu wel vermeden.

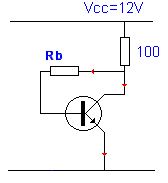
Een toepassing :

Veronderstel β gelijk aan 100.
Hoe groot is dan Rb voor een stroom van Ic = 10mA ?
We weten dat :

Vcc – Vbe
Ic = _________
Rc + (Rb/β)
Verander dit om Rb te kunnen bepalen.

Ic . (Re + (Rb/β)) = Vcc-Vbe

Vcc – Vbe Rb Vcc – Vbe
Re + (Rb/β) = _____________ ; ___ = ____________ – Re
Ic β Ic

Vcc – Vbe
Rb = β x ____________ – Re
Ic

Met cijfers : 100 x 12-0,7
________ – 100 = 103.000 Ω
0,01

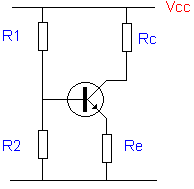
Een vierde methode: top of the bill !, de polarisatie door spanningsdeling :

Bekijk, bewonder en onthoud de fig. rechts:

Dit is de typische manier die je meestal in schema’s zal ontmoeten . Je merkt direct de spanningsdeler R1/R2 om de basisspanning te bepalen. Gezien vanuit de basis hebben we een deler, maar zoals je wel weet, kan volgens Thevenin (voor de berekeningen) dit geheel door één spanningsbron en één vervangings- weerstand voorgesteld worden. Voor de emitter gaat het om Re die een regelende functie bij de temperatuurverandering zal uitoefenen. De collector wordt door Rc belast.

In dit specifiek systeem is de ruststroom TOTAAL onafhankelijk van de winst β van de transistor.

We nemen de spanningsdeler onder de loep R1-R2:

We kunnen twee methoden toepassen:

1- De eerste bestaat uit het berekenen van de stroom doorheen R1 + R2 . Vervolgens de spanning over R2.
2- Hier gaan we volgens de verhouding van R1/R2 en vermenigvuldigen dan met de toegepaste spanning:

R2
Vb = _______ . Vcc
R1 + R2

Er komt geen magie bij te pas. De wet van Ohm, Thevenin, Norton en voila…

We kennen de vaste spanning op de basis Vb van de transistor. Wat is volgens jou nu de spanning op de emittor ?

Simpel : (ook over Re)

Ve = Vb -Vbe

De spanningen Ve, Vb zijn spanningen op de elektroden gemeten ten opzichte van de MASSA (NUL).

Vbe is een junctie spanning en dus 0,7 Volt. Daarmee kunnen we de stroom doorheen de emitter berekenen ( en bijgevolg ongeveer deze door de collector). Kijk hiernaast hoe eenvoudig dit is:

.

Ve
Ie = ______
Re

of
Vb – Vbe
Ie = _______
Re

Nooit meer vergeten:

Hoe is dit nu mogelijk ?
Op de basis staat een spanning bepaald volgens R1/R2.

Op de emitter vinden we deze spanning verminderd met Vbe of 0,7 V (dit is immers een diode ).

De stroom Ie = Ic + Ib, waarin Ib kan verwaarloosd worden aangezien deze zeer klein is. Aangepast hebben we Ic=Ie.

De wet van Ohm op de emittorweerstand toegepast:

De stroom doorheen Re de spanning over de klemmen gedeeld door de weerstand zelf, dus:

Ie = Ure / Re of

Ie = Ve / Re

Met andere woorden: het is wel degelijk Re die de stroom Ic bepaalt.

Een paar vuisregels bij dit type schakeling :

Niet direct wetenschappelijk maar eenvoudig:

– Voor een degelijke stabilisatie moet de spanningsval aan de klemmen van Re minstens 1 V bedragen (bij gebruik van een normale voedingsbron).

– De stroom door de spanningsdeler die Vbasis regelt, mag 5 à 10 maal die van de basis zelf zijn, zoniet zal de basisstroom zelf de deling beïnvloeden (denk eraan dat Ib ook door R1 vloeit).

Een voorbeeld met cijfers zal heel wat verduidelijken.

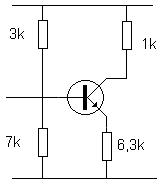
Links zie je deze schakeling: merk wel op dat de waarden van de weerstanden niet uit een E-reeks komen. Verder is de voedingsspanning 10 V.
We gaan alle spanningen en alle stromen in deze kring berekenen.

1 – berekenen we eerst de spanning die door de deler R1 (3K) en R2 (7K) wordt geleverd:

Reken maar:
R2
Vb = _______ . Vcc
R1 + R2

met gevolg:
7
Vb = ________ x 10 = 7V
10

2 – We berekenen de spanning op de emittor van de transistor:

Ve = Vb – Vbe
Ve = 7 – 0,7 = 6,3 V

3 – Vervolgens de stroom door de emittor, die eigenijk gelijk is aan de stroom door de collector:

Ie = Vre / Re
Ie = Ve / Re
Ie = 6,3 / 6300 = 0.001 A of 1 mA
de collector stroom voor Ib geregeld is ongeveer gelijk aan Ie

4 – Nu berekenen we de spanningsval over de collector weerstand:

U = Rc . Ic
We nemen Ic =Ie
Urc = 1000 X 0.001 = 1V

5 – Berekenen we Vce

Vce= Vcc – Rc.Ic – Re.Ie
Vce = 10 – 1 – 6.3 = 2,7 V

6 – Onze rust of instelspanning wordt als volgt bepaald:

Ic = 1 mA
Vce = 2.7V

7 – We bepalen de belastingslijn bij middel van de bijzondere (karakteristieke) sper- en verzadigingspunten :

Algemene vergelijking op de collector :
Vcc – (Rc.Ic + Vce + Re.Ie) = 0

Saturatiestroom:
Als Vce =0, Ic = Vcc/ (Rc + Re)
Ic voorVce=0 = 10/ 7300 = 1.37mA

Als Ic = 0 Vce =Vcc weze 10V

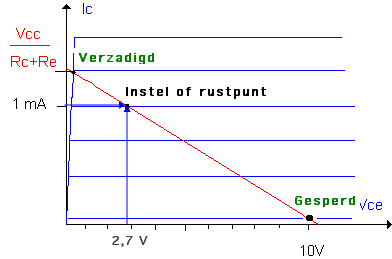
Het valt op dat het instelpunt niet optimaal geplaatst werd. Grotere signalen zullen vrij snel door het afknijpen van één alternantie vervormen . We doen er dus goed aan om dit rustpunt wat lager op de belastingslijn te plaatsen (liefst in het midden).
Om dit te realiseren is meer dan één oplossing mogelijk. We kunnen inspelen op de waarde van Re, waardoor Ic zal verminderen. Maar we kunnen ook op de spanningsdeler werken om een meer geschikt punt te bepalen.

Als conclusie onthouden we:

Als één en ander niet naar wens verloopt doen we er goed aan om de spanning op de emitter te meten.

Twee gevallen :

– We meten GEEN spanning. De transistor voert GEEN stroom. Aan jou om de reden te vinden. (is er wel voeding ? basisspanning ?…)

– Er staat wel een spanning. We delen die door de weerstand in de emitterkring en krijgen zo een idee van de stroom die er vloeit.

Bij toepassingen als spannings- of vermogensversterking zal men steeds een lineaire polarisatie (in het midden van de belastingslijn) betrachten. Slechts uitzonderlijk zal men naar een extreme instelling gaan, maar dat is een ander verhaal.