Het moet nu duidelijk zijn dat het gedrag van een weerstand bij wisselspanning toch niet identiek aan dit bij gelijkspanning zal zijn. Daarom dit hoofdstukje.
Princiepe schema :
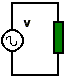
Hiernaast merken we een weerstand R die aan een wisselspanningsbron v gekoppeld is. We gaan er van uit dat het om een prima weerstand zonder inductief of capacitief gedrag gaat. Het gaat duidelijk om een ideale toestand, want elke echte component vertoont normaal ook een reactief gedrag naargelang de gebruikte frequentie ( spoel of condensator ).
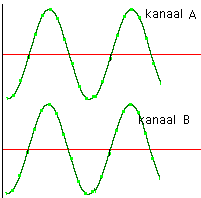
Bij deze proef gebruiken we een dubbelkanaalsoscilloscoop. Dat is hier nodig omdat we twee signalen willen bekijken en vergelijken. Het kanaal A sluiten we op de bron zelf aan, het kanaal B aan de weerstand zelf (we zien hierdoor de stroom).
In de praktijk is deze opstelling niet mogelijk.
Dat we de stroom bekijken omdat kanaal B aan de weerstand hangt, volgt uit het feit dat de stroom “I” een spanningsval veroorzaakt.
Door de twee kanalen van de scoop kunnen we “gelijktijdig” de twee fenomenen zien.
Wat zien we ?
Door in te werken op de versterking van elk kanaal kunnen we de proef zo regelen dat beide signalen perfect over elkaar heen komen te liggen. We kunnen op dat moment naar één signaal kijken.
Interpretatie :
We onthouden :
Doordat beide signalen perfect over elkaar passen, kunnen we besluiten dat er GEEN tijdverschil tussen beide bestaat. Met andere woorden, stroom en spanning verschijnen duidelijk simultaan en dit op elk moment.
Een ideale weerstand heeft geen enkele invloed op het tijdsgebeuren bij wisselstroom. Men zegt ook dat : U en I steeds in fase verkeren.
Hieruit volgt :
I= U / R
Men zegt dan dat: de “impedantie” van een weerstand gelijk aan de weerstand zelf is.
Hierin zijn U en I de effectieve waarden en R in W uitgedrukt.
Het opgenomen vermogen is :
P = U * I
P = R * I2
Je merkte het al, we voeren een nieuwe uitdrukking in nl: de impedantie.
De impedantie is gelijk aan de verhouding van de amplitude van de spanningen tot de amplitude van de stroom in de kring.
Dit alles om te stellen dat de impedantie van een zuivere weerstand R eigenlijk gelijk aan de weerstand bij wisselstroom is.
Waarom dan nog een bijzondere naam gebruiken ?
We zien verder wel dat “weerstand bieden aan stroom” niet enkel met een weerstand gebeurt. Wel is zo dat de weerstand vermogen verbruikt ( omzet in warmte ). We zullen zien dat dit bij de spoel en de condensator wel anders ligt.
Hoe kunnen we dit nu grafisch voorstellen ?
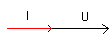
Het gaat hier om de vectorvoorstelling. Stroom en spanning konden we door vectoren voorstellen ( dat hadden we al gezien ). U en I zijn twee lijntjes waarvan men de richting aangeduid door het pijltje. Aangezien beiden steeds in fase met elkaar zijn, bevinden beide vectoren zich over elkaar. De grootte stelt de amplitude voor van de effectieve waarde.
Defasering nul.

