Weerstanden in serie

Het kan voorkomen dat je geschakelde weerstanden moet gebruiken. Om bepaalde redenen kunnen die zowel in serie als in parallel met elkaar geschakeld worden. Wat is dan het resultaat ?

Werkwijze :

We plaatsen twee weerstanden, één van 10 kΩ en één van 4,7kΩ na elkaar. Zie het schema hiernaast. Hoe moeten we het totaal bepalen (of de vervangingsweerstand)?

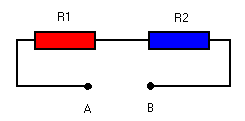
Het is eenvoudig te begrijpen dat een stroom die wordt afgeremd in de eerste weerstand ook in de tweede geremd zal worden. Het stroomdebiet verkleint nogmaals. Dit komt neer op een vergroting van de weerstand. De berekening hiernaast verduidelijkt dit.

In ons voorbeeld:

Wees er zeker van dat je de eenheidswaarde genormaliseerd hebt. Met andere woorden: je kan niet zomaar kΩ met Ω samentellen als je niet bv. kΩ herleid hebt naar Ω of andersom.

Rt = 10 000 + 4700 = 14 700 Ω of 14,7 kΩ

Stel nu dat we 5 weerstanden achter elkaar schakelen :

Geen probleem, het resultaat wordt dan : Rt = R1 + R2 + R3 + R4 + R5.

Wat is nu de stroom door zo een kring ?

Passen we de wet van Ohm toe op dit voorbeeld met twee weerstanden.

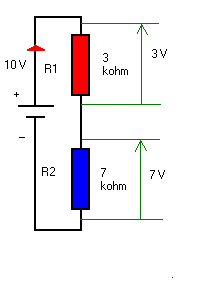
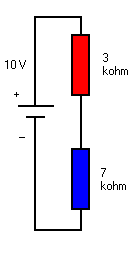
Goed, de opstelling ziet er nu als op de tekening hiernaast uit. We merken een bron (of generator) van 10 V, een weerstand van 3 kΩ in serie met één van 7 kΩ.

Berekenen we eerst de totale waarde van beide weerstanden in serie:

Rt = R1 + R2
Rt = 3000 + 7000 = 10 000 Ω of 10 kΩ

Dit was reeds bekend.

Berekenen we nu de stroom door de kring:

Toepassen van de Wet van Ohm

I = U / R
I = 10/10 000 = 0,001 A = 1. 10-3 A = 1 mA

(Word nu reeds gewoon aan de wetenschappelijke notatie !!)

Een zelfde stroom vloeit door de 3 kΩ en de 7 kΩ weerstanden.
We gaan nu de spanningen over elke weerstand bepalen. De bron blijft 10 V. Deze spanning wordt over de twee weerstanden verdeeld.

Hoe te werk gaan ?

Toepassen van de wet van Ohm. U = R I.

1 – Over de weerstand van 3 kΩ

U = R I

U = 3000 x 0.001 = 3 V

2 – Over de weerstand van 7 kΩ

U = R I

U = 7000 x 0.001 = 7 V

Fundamenteel ! (nogmaals)

Met dit opzet hebben we een schakeling gemaakt (3 V enerzijds en 7 V anderzijds). Deze schakeling wordt daarom spanningsdeler genoemd
De stroom van 1 mA vloeit door gans de kring, hij is op elk punt gelijk.

De rode pijl wijst op de richting van de stroom. Bij conventie heeft men die van + naar – genomen. ( In werkelijkheid lopen de elektronen juist andersom. )

De spanning over de klemmen van elke weerstand is evenredig met de waarde van die weerstand. De spanningsval gebeurt eveneens bij conventie van + naar –

Tot slot …

Is het nodig om de spanningsval over elke weerstand te berekenen ?

Niet echt, het volstaat de verhouding (proportionaliteit) van de spanningsdeling te bepalen.