Wisselstroom: effectieve waarde

Bij wisselstroom ( of spanning) hebben we gezien dat de stroom of spanningswaarde continu verandert. Als het er op aan komt energie te ontwikkelen zal je gemakkelijk begrijpen dat dit niet op een zelfde manier als met gelijkstroom of -spanning zal gaan. Hier bekijken we hoe het Joule-effect correct bepaald kan worden.

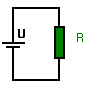
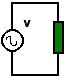
Vergelijk beide tekeningen :

Een weerstand R verwerkt een gelijkstroom en ontwikkelt warmte.

Een stroom I = U/R volgt volgens de wet van Ohm. Door het Joule-effekt ontstaat warmte in de weerstand.

Hierboven wordt wisselstroom gebruikt. De weerstand zal eveneens opwarmen. Hoeveel ?

Een stroom  I = V/R zal vloeien, en ook hier onstaat warmte door het Joule effekt in de weerstand.

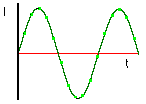
De vorm van de stromen

Uit de figuren ziet men duidelijk dat er een verschil MOET bestaan tussen beide vormen en hun effect. Gedurende een bepaalde tijd zal de warmte die de gelijkstroom ontwikkelt, groter zijn dan die door wisselstroom. We hebben nood aan een coëfficiënt die de relatie tussen gelijk- en wisselstroom vastlegt. Het zal duidelijk zijn dat het hier om een sinusoïdale vorm gaat. Merk verder ook op dat tijdens de negatieve fase, de zin van de stroom omgekeerd wordt.

Als antwoord kunnen we stellen:

De energie, de warmte die in een weerstand wordt ontwikkeld, wordt bepaald door de effektieve waarde van de signaalvorm aangelegd aan de weerstand. In dit geval een sinusvormige wisselspanning en een gelijkspanning.

Bepaling van Ieff en Ueff

Vertrekkend van wat we op de oscilloscoop gezien hebben: als we de maximum of piekwaarde kennen, wordt deze factor voor een sinus :

We weten allemaal dat de vierkantswortel van 2 = 1,41

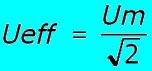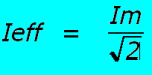Belangrijk :

De bij ons geleverde netspanning bedraagt 230 V AC maar in effectieve waarde uitgedrukt . Het toestel waarmede we deze netspanning kunnen meten werd in effectieve waarde gekalibreerd ( streepjes op de afleesschaal geplaatst ).

Maak er daarom een gewoonte van om van effektieve waarde te spreken.

Uitermate belangrijk en dus herhaald:

-) De redenering hiervoor gaat enkel op voor sinusvormige signalen !!!

-) Wat nu met gelijkspanning ? Daarvoor kan men stellen dat de factor in de formule, niet meer de vierkantswortel van 2, maar gewoon het getal 1 is en dus niets in de formule bijbrengt. Gelijkspanning is dus eenvoudigweg de referentievorm.

Daarom kan men volgende uitdrukking gebruiken: De effektieve waarde is die waarde die een gelijkspanning aan vermogen in vervanging van de sinus zou leveren. ( piekwaarde gedeeld door 1,41 geeft de effectieve gelijkspanning )

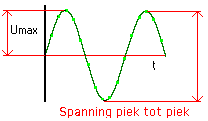
Opgelet, vermijd de volgende verwarring :

U max is NIET het zelfde als Vpp ( of “peak to peak” ).

Nog een voorbeeld :

We meten met een oscilloscoop een spaning V pp van 648 V. Welke zijn nu de Vmax en de Veff (effectief) ?

Eenvoudig: de maximum spanning is duidelijk de helft van de Upp.

Umax =  Upp / 2 =   648/2 = 324 V
Ueff = Um / (wortel 2) =  324/1,41 = 230V